Depth of Focus(DOF)는 광학에서 이미지가 허용 가능한 초점 내에서 유지되는 범위를 나타냅니다. 우리 말로 초점 심도라고 하는 DOF는 주로 개구수(NA: Numerical Aperture), 해상도(Resolution), 그리고 공정에서 사용하는 경험적 상수 K2와 밀접한 관계가 있습니다.
1. DOF의 정의
DOF는 초점 위치가 약간 변해도 이미지 품질이 허용 범위 내에서 유지되는 깊이를 나타냅니다. 높은 해상도를 가진 광학 시스템에서는 DOF가 짧아지며, 이는 초점 맞추기가 더 까다로움으로 이어집니다.
2. DOF와 NA의 관계
NA는 렌즈의 수치 개구수를 나타내며, 다음 공식으로 정의됩니다. 여기서 말하는 개구수란 빛을 받아 들일 수 있는 정도를 의미합니다. 개구수가 높다는 것은 빛을 많이 받아 들일 수 있다는 것으로 해석할 수 있습니다.
$$NA=n⋅sin(θ)$$
- n: 매질의 굴절률
- θ: 렌즈의 반 개구각
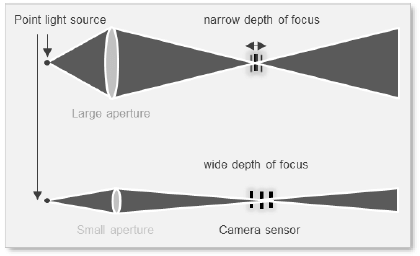
아래의 그림에서 위의 그림이 NA가 커지면서 초점을 맞출 수 있는 초점 심도가 작이지면서 조정하는 것이 힘들어지는 것을 알 수 있습니다.
아래 부분은 초점 심도가 커져서 초점을 맞출 수 있는 범위가 크다는 것을 알 수 있지만, 한눈에 봐도 들어오는 빛의 양이 적은 것을 알 수 있습니다.
DOF는 NA와 반비례 관계에 있습니다. 이는 다음과 같은 수식으로 표현됩니다. 이 수식은 매우 유명한 수식이기 때문에 꼭 외워두거나 알아 두시기 바랍니다.
$$DOF = \frac{K_2 \cdot \lambda}{NA^2}$$
- $K2$: 경험적 상수
- $λ$: 사용된 광원의 파장
즉, NA가 커질수록 DOF는 감소하여 초점 깊이가 얕아집니다. 이는 고해상도 시스템에서 특히 필요로 하는 설계 요소입니다.
3. DOF와 파장(λ)의 관계
Depth of Focus(DOF)는 사용된 광원의 파장(λ)에 직접적인 영향을 받습니다. 파장이 짧아질수록 DOF가 안 좋아지며, 고해상도 광학 시스템에서 마찬가지로 중요한 설계 요소가 됩니다. DOF와 파장의 관계는 아래 수식으로 표현됩니다.
$$\frac{K_2 \cdot \lambda}{NA^2}$$
주요 포인트
- 짧은 파장: λ가 짧아지면 DOF가 작아져 초점이 더 얕아집니다. 이는 해상도를 높이기 위해 짧은 파장(EUV 13.5nm) 을 사용하는 시스템에서 정밀한 초점 제어가 필요함을 의미합니다.
- 긴 파장: λ가 길어지면 DOF가 깊어져 초점 허용 범위가 넓어집니다. 이는 저해상도 환경(192nm Laser) 에서는 안정적인 초점 유지에 유리합니다.
예시
- 사용된 파장이 $λ$=500nm일 때, NA = 0.9, $K2$=0.5라면 $$DOF = \frac{0.5 \cdot 500 \, \text{nm}}{0.9^2} \approx 308 \, \text{nm}$$
- 파장이 $λ$=300 nm로 짧아진 경우DOF
$$\frac{0.5 \cdot 300 \, \text{nm}}{0.9^2} \approx 185 \, \text{nm}$$
결론
파장이 짧아질수록 DOF는 줄어들며, 이는 고해상도 요구 사항을 충족하기 위한 설계 요소로 작용합니다. 따라서, 광학 시스템에서 파장 선택은 DOF와 해상도 간의 균형을 결정하는 핵심 변수입니다.
4. DOF와 Resolution(해상도)의 관계
해상도는 Rayleigh 기준에 의해 다음과 같이 계산됩니다. 해상도가 좋다는 말은 분해능(물질을 잘게 쪼갤 수 있는 능력)이 좋다는 말이기 때문에 R의 값이 작아질 수록 좋은 것입니다. $K1$상수와 $K2$ 상수는 다른 것입니다.
$$R = \frac{K_1 \cdot \lambda}{NA}$$
- $K1$: 공정 상수
- $λ$: 광원의 파장
DOF와 해상도는 서로 밀접한 관련이 있습니다. 해상도가 좋아질수록(R의 값이 작아질 수록) NA가 커지며, 이로 인해 DOF가 감소합니다. 따라서 해상도를 높이려면 더 정밀한 초점 심도 조정이 필요합니다.
5. $K2$ 상수의 역할
$K2$는 DOF의 크기를 조정하는 경험적 상수로, 시스템 설계와 공정 조건에 따라 달라질 수 있습니다:
- $K2$가 작을수록 DOF가 감소합니다.
- $K2$가 클수록 DOF가 증가하지만, 이는 해상도 감소를 동반할 수 있습니다.
공정의 정확도를 높이고 시스템을 최적화하려면 $K2$ 상수를 적절히 선택하는 것이 중요합니다.
6. 결론: NA, Resolution, K2의 상호작용
- NA 증가: 해상도 증가, DOF 감소
- $K2$ 조정: DOF를 조정하여 시스템 최적화
- Resolution 증가: 더 얕은 DOF 요구
| 적용 | 효과 | 효과 |
| $λ$ ⬇ | Resoultion ⬆ | DOF ⬇ |
| NA ⬆ | Resolution ⬆ | DOF ⬇⬇ |
표에서 볼 수 있듯이 NA와 해상도가 높을수록 더 정밀한 초점 제어가 필요하며, DOF는 훨씬 짧아집니다. 설계 시 이 요소들을 균형 있게 고려해야 합니다.
6. 수식의 예시
아래는 DOF 계산을 위한 공식의 예입니다.
$$2DOF = \frac{K_2 \cdot \lambda}{NA^2}$$
여기서, $K2$=0.5 $λ$=500 nmNA=0.9일때.
$$DOF = \frac{0.5 \cdot 500 \times 10^{-9}}{0.9^2} \approx 308 \, \text{nm}$$
7. 시각적 이해
NA와 DOF 간의 반비례 관계를 시각적으로 이해하려면 그래프를 활용할 수 있습니다. 예를 들어, NA가 증가할수록 DOF가 감소하는 패턴을 확인할 수 있습니다.
DOF와 NA의 그래프

Y축: DOF (Depth of Focus) / X축: NA (Numerical Aperture)